Restricted Choice and Math
#1

Posted 2016-July-22, 16:26
#2

Posted 2016-July-22, 17:15
 Spisu, on 2016-July-22, 16:26, said:
Spisu, on 2016-July-22, 16:26, said:
There's absolutely nothing odd about focusing on finessing the ten. Because that is your alternative play for getting a trick. After the first play to the Q loses, on the second round you have a choice of finessing against the ten or playing for the other of the A or K to be onside. The article is demonstrating that the odds of playing the J on the second round is superior to finessing against the ten. 2:1 on the hands that matter (not counting hands where either works or both fail).
Quote
And the argument is made that it's 2:1 odds to be a lone honor since Aces and Ks played from double honors are shown to appear at 1/2 the frequency of lone honors. RC logic appears verified.
Then I saw the data showed East winning only 500 first finesses when it should be 600 of 800 hands (75%). Checking the text, the author noted he had excluded some hands (200) from the data, saying they made no difference. I had read that and took it at face value. But here, you also always lose to E's lone honors and the double honors, which WERE included. **And isn't the whole issue in a Restricted Choice proof to show your losses to all specific honors in East's hands to compare their frequency?**
The table is charting the location of the ace, the king, AND THE TEN. Not just the ace and king! It is excluding the cases of AKT onside (where any strategy works), and AKT offside (where any strategy fails). It is showing all distributions where one hand holds 2 of the 3 honors, which are all equal in frequency. The hands where all 3 honors are in one hand are somewhat less in frequency (so if you wanted to accurately include them in the table it should be only like 84.6 instead of 100 for the other cases). But since strategy is irrelevant on those they were omitted from the table.
Quote
It's excluding the losses to AKT offside, where playing the 9 second round would also fail. The point of this example is to compare the odds of finessing against the ten vs. playing for split ace and king.
Basically there are two methods of reasoning to show that playing for split honor is better. Despite your insistence, neither is fallacious.
1. RHO is dealt Kt and AT alone (in terms of honors, with or without additional small cards) twice as often as AK alone. So playing for split A/K is twice as successful on the hands that matter. 200 to 100, counting both hands where the ace was won first round and hands where the K was won first round (Ignoring KT and AT onside where anything works)
2. Say RHO won the K the first time. So on the hands that matter, either he was dealt the KT (which he will be 100 times), or he was dealt the AK AND HE CHOSE TO PLAY THE KING. Which he will do 50 times. So again, the conclusion is that playing for split honors will work 2:1. 100 to 50, counting only hands where the K was won first round.
#4

Posted 2016-July-23, 03:33
 Stephen Tu, on 2016-July-22, 17:15, said:
Stephen Tu, on 2016-July-22, 17:15, said:
The table is charting the location of the ace, the king, AND THE TEN. Not just the ace and king! It is excluding the cases of AKT onside (where any strategy works), and AKT offside (where any strategy fails). It is showing all distributions where one hand holds 2 of the 3 honors, which are all equal in frequency. The hands where all 3 honors are in one hand are somewhat less in frequency (so if you wanted to accurately include them in the table it should be only like 84.6 instead of 100 for the other cases). But since strategy is irrelevant on those they were omitted from the table.
It's excluding the losses to AKT offside, where playing the 9 second round would also fail. The point of this example is to compare the odds of finessing against the ten vs. playing for split ace and king.
Basically there are two methods of reasoning to show that playing for split honor is better. Despite your insistence, neither is fallacious.
1. RHO is dealt Kt and AT alone (in terms of honors, with or without additional small cards) twice as often as AK alone. So playing for split A/K is twice as successful on the hands that matter. 200 to 100, counting both hands where the ace was won first round and hands where the K was won first round (Ignoring KT and AT onside where anything works)
2. Say RHO won the K the first time. So on the hands that matter, either he was dealt the KT (which he will be 100 times), or he was dealt the AK AND HE CHOSE TO PLAY THE KING. Which he will do 50 times. So again, the conclusion is that playing for split honors will work 2:1. 100 to 50, counting only hands where the K was won first round.
#5

Posted 2016-July-23, 04:49
 Stephen Tu, on 2016-July-22, 17:15, said:
Stephen Tu, on 2016-July-22, 17:15, said:
The table is charting the location of the ace, the king, AND THE TEN. Not just the ace and king! It is excluding the cases of AKT onside (where any strategy works), and AKT offside (where any strategy fails). It is showing all distributions where one hand holds 2 of the 3 honors, which are all equal in frequency. The hands where all 3 honors are in one hand are somewhat less in frequency (so if you wanted to accurately include them in the table it should be only like 84.6 instead of 100 for the other cases). But since strategy is irrelevant on those they were omitted from the table.
It's excluding the losses to AKT offside, where playing the 9 second round would also fail. The point of this example is to compare the odds of finessing against the ten vs. playing for split ace and king.
Basically there are two methods of reasoning to show that playing for split honor is better. Despite your insistence, neither is fallacious.
1. RHO is dealt Kt and AT alone (in terms of honors, with or without additional small cards) twice as often as AK alone. So playing for split A/K is twice as successful on the hands that matter. 200 to 100, counting both hands where the ace was won first round and hands where the K was won first round (Ignoring KT and AT onside where anything works)
2. Say RHO won the K the first time. So on the hands that matter, either he was dealt the KT (which he will be 100 times), or he was dealt the AK AND HE CHOSE TO PLAY THE KING. Which he will do 50 times. So again, the conclusion is that playing for split honors will work 2:1. 100 to 50, counting only hands where the K was won first round.
Removed by author
#6

Posted 2016-July-23, 05:09
 Spisu, on 2016-July-22, 16:26, said:
Spisu, on 2016-July-22, 16:26, said:
To what end?
#7

Posted 2016-July-23, 05:56
 sfi, on 2016-July-22, 18:00, said:
sfi, on 2016-July-22, 18:00, said:
You reminded me of this news
http://worldnewsdail...-yet-not-human/
#8

Posted 2016-July-23, 06:12
Psyche (pron. sahy-kee): The human soul, spirit or mind (derived, personification thereof, beloved of Eros, Greek myth).
Masterminding (pron. m
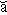 s
s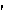 t
t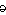 r-m
r-m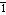 nd
nd ing) tr. v. - Any bid made by bridge player with which partner disagrees.
ing) tr. v. - Any bid made by bridge player with which partner disagrees."Gentlemen, when the barrage lifts." 9th battalion, King's own Yorkshire light infantry,
2000 years earlier: "morituri te salutant"
"I will be with you, whatever". Blair to Bush, precursor to invasion of Iraq
#9

Posted 2016-July-23, 06:19
 Spisu, on 2016-July-22, 16:26, said:
Spisu, on 2016-July-22, 16:26, said:
 Spisu, on 2016-July-22, 16:26, said:
Spisu, on 2016-July-22, 16:26, said:
Psyche (pron. sahy-kee): The human soul, spirit or mind (derived, personification thereof, beloved of Eros, Greek myth).
Masterminding (pron. m
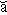 s
s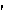 t
t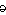 r-m
r-m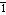 nd
nd ing) tr. v. - Any bid made by bridge player with which partner disagrees.
ing) tr. v. - Any bid made by bridge player with which partner disagrees."Gentlemen, when the barrage lifts." 9th battalion, King's own Yorkshire light infantry,
2000 years earlier: "morituri te salutant"
"I will be with you, whatever". Blair to Bush, precursor to invasion of Iraq
#10

Posted 2016-July-23, 06:28
#11

Posted 2016-July-23, 10:25
 Spisu, on 2016-July-23, 04:49, said:
Spisu, on 2016-July-23, 04:49, said:
Uh:
- You didn't actually show anything to be incorrect
- The point of the example is not solely to address East's play of equal honors. It is to address what is the better play on the second round after the first trick has been lost to the ace or king, finessing LHO for the ten, or playing LHO for the other of the ace or king.
Quote
OK, without the ten, the complete chart, omitting small cards, and using 1000 deals so I can be more accurate and stick to integers:
West East AK - 240 A K 260 K A 260 - AK 240
So 260 times you lose to the K from K alone from East, 120 times you lose to the K from AK from east.
260 times you lose to the A from A alone from East, 120 times you lose to the A from AK from east.
But this table doesn't really give you anything to compare vs. finessing the ten, because the ten isn't listed here. In real life, playing for split A/K, you succeed when west has at least one of the A/K (76%), and when west has the stiff T or doubleton Tx (3.39% combined). So 79.39% for the strategy of low to the Q, low to the J.
With the ten, complete chart:
West East AKT - 110 AK T 130 AT K 130 KT A 130 A KT 130 K AT 130 T AK 130 - AKT 110
The ACBL encyclopedia chart is basically omitting the first and last lines of my table because they are irrelevant for the purposes of comparing line vs. 2nd round finesse of the ten (not irrelevant for counting how often east has both highest honors vs. not having both highest honors, but that is not what the article is trying to do, it is not trying to calculate the same thing you are). And they are using 100 for the cases in the middle instead of 130, which is fine since all of these are equal frequency.
This table agrees with the table omitting the T. If you take losing to the K as the example:
lose to K from AK not the T, half of 130 = 65.
lose to K from AK and the T, half of 110 = 55.
total losing to K the AK with or without the T: 120
lose to K holding K only, no T, no A = 130
lose to K holding K & T, no A = 130:
total losing to the K without the A: 260
Note this is giving the same numbers, 260:120 as I gave in the table omitting the T, it's the same deals just being more specific about where the T is.
So, looking at the complete chart, again we see if playing West for A or K we win 79.39% of the time, when west has at least one of the A/K or exactly stiff T or doubleton Tx. Finessing the T on the second round instead, we win 50% of the time when the T was onside, and additionally we win 13% of the time when West has the AK without the ten (the first play to the Q held). We also pick up an additional 6.78% when West has the stiff A, stiff K, Ax, or Kx, because a high honor will pop up first or second time we play the suit. So the overall success rate for the alternate line is 69.78%, worse than playing West to have one of the A/K by about 9.6%. These lines have a lot of overlap, there are a lot of combos where both win, and both lose. If you are looking at only the lines of the table where what you do actually can make a difference, the only relevant entries are:
A KT 130 K AT 130 T AK 130
Out of these, close to 34 times out of each, west will show up with their lone honor stiff or doubleton and relieve you of guessing, so we are left with:
A(xx/xxx/xxxx) KT(xx/x/-) 96 K(xx/xxx/xxxx) AT(xx/x/-) 96 T (xx/xxx/xxxx) AK(xx/x/-) 96
And again, the reasoning is either
1. Count both losing to the ace and losing to the K first round, count all of these entries. So out of the relevant entries you are winning 19.2% vs. 9.6% to play A/K onside 2nd round instead of finesse vs. ten, 2:1 in favor of playing for split A/K on the hands where your play matters. You compare table entries 1&2 vs. 3. This is where we get the 9.6% overall edge for the split A/K line over finesse the 9 2nd round. All the other cases are equal.
2. Only count instances where we lost first round to the K, so only count the second line, and only half of the third line, because half the time from AK RHO will play the ace. Paying attention to half the cases of 1, only ones where the K was won first round. You compare table entry 2 vs. half of 3. If you want to look at times RHO won the ace, you instead compare table entry 1 to the other half of 3. Combined, it's just the same as reasoning 1. There's nothing fallacious about identifying which honor RHO won with. You just are looking at half the cases.
#12

Posted 2016-July-23, 14:55
 Stephen Tu, on 2016-July-23, 10:25, said:
Stephen Tu, on 2016-July-23, 10:25, said:
- You didn't actually show anything to be incorrect
- The point of the example is not solely to address East's play of equal honors. It is to address what is the better play on the second round after the first trick has been lost to the ace or king, finessing LHO for the ten, or playing LHO for the other of the ace or king.
OK, without the ten, the complete chart, omitting small cards, and using 1000 deals so I can be more accurate and stick to integers:
West East AK - 240 A K 260 K A 260 - AK 240
So 260 times you lose to the K from K alone from East, 120 times you lose to the K from AK from east.
260 times you lose to the A from A alone from East, 120 times you lose to the A from AK from east.
But this table doesn't really give you anything to compare vs. finessing the ten, because the ten isn't listed here. In real life, playing for split A/K, you succeed when west has at least one of the A/K (76%), and when west has the stiff T or doubleton Tx (3.39% combined). So 79.39% for the strategy of low to the Q, low to the J.
With the ten, complete chart:
West East AKT - 110 AK T 130 AT K 130 KT A 130 A KT 130 K AT 130 T AK 130 - AKT 110
The ACBL encyclopedia chart is basically omitting the first and last lines of my table because they are irrelevant for the purposes of comparing line vs. 2nd round finesse of the ten (not irrelevant for counting how often east has both highest honors vs. not having both highest honors, but that is not what the article is trying to do, it is not trying to calculate the same thing you are). And they are using 100 for the cases in the middle instead of 130, which is fine since all of these are equal frequency.
This table agrees with the table omitting the T. If you take losing to the K as the example:
lose to K from AK not the T, half of 130 = 65.
lose to K from AK and the T, half of 110 = 55.
total losing to K the AK with or without the T: 120
lose to K holding K only, no T, no A = 130
lose to K holding K & T, no A = 130:
total losing to the K without the A: 260
Note this is giving the same numbers, 260:120 as I gave in the table omitting the T, it's the same deals just being more specific about where the T is.
So, looking at the complete chart, again we see if playing West for A or K we win 79.39% of the time, when west has at least one of the A/K or exactly stiff T or doubleton Tx. Finessing the T on the second round instead, we win 50% of the time when the T was onside, and additionally we win 13% of the time when West has the AK without the ten (the first play to the Q held). We also pick up an additional 6.78% when West has the stiff A, stiff K, Ax, or Kx, because a high honor will pop up first or second time we play the suit. So the overall success rate for the alternate line is 69.78%, worse than playing West to have one of the A/K by about 9.6%. These lines have a lot of overlap, there are a lot of combos where both win, and both lose. If you are looking at only the lines of the table where what you do actually can make a difference, the only relevant entries are:
A KT 130 K AT 130 T AK 130
Out of these, close to 34 times out of each, west will show up with their lone honor stiff or doubleton and relieve you of guessing, so we are left with:
A(xx/xxx/xxxx) KT(xx/x/-) 96 K(xx/xxx/xxxx) AT(xx/x/-) 96 T (xx/xxx/xxxx) AK(xx/x/-) 96
And again, the reasoning is either
1. Count both losing to the ace and losing to the K first round, count all of these entries. So out of the relevant entries you are winning 19.2% vs. 9.6% to play A/K onside 2nd round instead of finesse vs. ten, 2:1 in favor of playing for split A/K on the hands where your play matters. You compare table entries 1&2 vs. 3. This is where we get the 9.6% overall edge for the split A/K line over finesse the 9 2nd round. All the other cases are equal.
2. Only count instances where we lost first round to the K, so only count the second line, and only half of the third line, because half the time from AK RHO will play the ace. Paying attention to half the cases of 1, only ones where the K was won first round. You compare table entry 2 vs. half of 3. If you want to look at times RHO won the ace, you instead compare table entry 1 to the other half of 3. Combined, it's just the same as reasoning 1. There's nothing fallacious about identifying which honor RHO won with. You just are looking at half the cases.
Removed by author
#13

Posted 2016-July-23, 15:22
 Spisu, on 2016-July-23, 14:55, said:
Spisu, on 2016-July-23, 14:55, said:
You keep on saying "800 hands of play". Nowhere in the article does it ever claim it is analyzing 800 hands. It is analyzing *600* hands, not *800* hands, and is specifically ignoring cases where West has AKT, and cases where East has AKT. East will indeed win 500/600 hands first trick when those are excluded (and we decide for simplicity to ignore the extremely rare 0.48%*2 cases where west has a stiff A or K and it pops up on round 1). If it were to include those hands, if it were doing accurate correct proportions, and the other cases are 100 hands each (for 2 out of 3 honors), then it should be analyzing 769.23 hands, not 800, because the AKT holdings are only 11/13 as common as the 2 out of 3 honor holdings. East would win first trick 584.6/769.23 or 76% of the time. Or they could have done the table like I did, analyze 1000 hands, not 600 or 800, and the accurate numbers of 110 for AKT in one hand holdings, 130 for 2 out of the 3 honors. East would have at least one of A or K 760/1000 times. Those are the actual correct numbers given the constraints of 13 cards to a hand. East has at least one of ace or K 76% of the time not 75.
But for the sake of simplicity let's ignore this small error and allow you a hypothetical 800 hands of play including 100 each of AKT onside and AKT offside even though that's a bit high.
Quote
No, they don't equalize. From their table:
A KT 100
K AT 100
AT K 100
KT A 100
That's 400 cases where lone A/K (with or without the T) wins first trick. 200 cases where specifically the lone K wins first trick.
T AK 100 (50 each for A and K winning first round)
- AKT 100 (50 each for A and K) (in reality this should be 84.6, 42.3 each for ace and king)
200 cases given your overestimation of the AKT omitted combo. 184.6 in real life.
400:200, ~2:1 for lone A/K vs. double A/K. Not equalized. 2.167:1 if wanting more accuracy.
Or also ~2:1 for lone K winning vs. K winning from double A/K. Not equalized.
I think you apparently forgot to count both
AT K
and
A KT
as separate cases in your original post which leads to your incorrect conclusions about the validity of the article. That's 200 times where the K without the ace wins K, not 100 as your original post says.
Quote
So, I take the time to carefully break down every combination for you and give you precise numbers for everything. You don't bother to dispute any of my figures whatsoever, and brush everything away with meaningless "you are filibustering", completely unable to point out where my numbers go wrong. I give up, go ahead and wallow in your ignorance.
#14

Posted 2016-July-23, 21:06
 Stephen Tu, on 2016-July-23, 15:22, said:
Stephen Tu, on 2016-July-23, 15:22, said:
But for the sake of simplicity let's ignore this small error and allow you a hypothetical 800 hands of play including 100 each of AKT onside and AKT offside even though that's a bit high.
No, they don't equalize. From their table:
A KT 100
K AT 100
AT K 100
KT A 100
That's 400 cases where lone A/K (with or without the T) wins first trick. 200 cases where specifically the lone K wins first trick.
T AK 100 (50 each for A and K winning first round)
- AKT 100 (50 each for A and K) (in reality this should be 84.6, 42.3 each for ace and king)
200 cases given your overestimation of the AKT omitted combo. 184.6 in real life.
400:200, ~2:1 for lone A/K vs. double A/K. Not equalized. 2.167:1 if wanting more accuracy.
Or also ~2:1 for lone K winning vs. K winning from double A/K. Not equalized.
I think you apparently forgot to count both
AT K
and
A KT
as separate cases in your original post which leads to your incorrect conclusions about the validity of the article. That's 200 times where the K without the ace wins K, not 100 as your original post says.
So, I take the time to carefully break down every combination for you and give you precise numbers for everything. You don't bother to dispute any of my figures whatsoever, and brush everything away with meaningless "you are filibustering", completely unable to point out where my numbers go wrong. I give up, go ahead and wallow in your ignorance.
You're right. My apologies. I did misread those 100 100 50 numbers as being for A K and A-K. And the oddity of adding in a frequency distribution for a single card finesse, the 200 omitted hands, and the 500 wins of a first finesse (450 is max in 600 hands and 600 right for 800, so it is wrong either way) all raised red flags.
But unfortunately, the one absurdity that slipped by me was the chart figure showing a four to one ratio between wins by lone honors to those from double honors (200 to 50). So it's still a terrible example to supposedly prove a point...I will try to edit out the initial post.
#15

Posted 2016-July-24, 07:47
#16

Posted 2016-July-24, 08:48
 Spisu, on 2016-July-23, 21:06, said:
Spisu, on 2016-July-23, 21:06, said:
But unfortunately, the one absurdity that slipped by me was the chart figure showing a four to one ratio between wins by lone honors to those from double honors (200 to 50). So it's still a terrible example to supposedly prove a point...I will try to edit out the initial post.
All those things you consider odd, absurd, terrible are because you are not grasping what question the article is trying to answer. You assume they are trying to answer your own question, when the article is addressing a completely different question.
You are apparently obsessed with the question
"what is the success percentage for leading toward the Q and then the J, considering all possible layouts? I don't care about the damn ten because that's irrelevant".
And think that is the only question worth asking, apparently, and assume the article is calculating this even when the text of the article clearly ignores this.
But the article is *not* trying to answer that question. Nowhere in the article does it claim it is trying to. It never says that this line succeeds 76% of the time or 79% of the time or whatever.
It is answering the quite different question:
"on the second round, after having lost to the K or A, is it better to play low to your jack, or to finesse the 9? I only care about layouts where it makes a difference, one choice wins while the other loses, and the ten is important since I am considering finessing the 9".
It is not trying to calculate success percentages overall on all layouts. It is just exploring on which layouts playing to a high honor is better than finessing the 9, and which layouts finessing the 9 is better. That's why it omits so many layouts, and is unconcerned about how many times it depicts East winning from all 3 honors. It is not concerned about the same things you are, because it is asking a different question!
The point of the article is to educate the person who has not considered the effect of an opponent having choice of plays. A naive bridge player not exposed to this concept might see that opponent won first trick with K. They saw the K, therefore the chance of A alone is zero. They reason that the only layouts that matter are AK without the ten offside, and KT without the ace offside. These layouts are dealt equally originally. They may then erroneously conclude that the second round play is just a tossup guess. It isn't, because the opponent has choice of plays which drastically reduces the chances of one of those layouts.
#17

Posted 2016-July-24, 14:37
The bidding tells me a little bit about opps hand distribution so the a priori odds of 11/6 (assuming Gib plays randomly with QJ) on west's jack being a singleton no longer holds. It looked like clubs split 6-3. So west's distribution would be either 9-1 or 8-2 in the pointies and hearts. The a priori odds of 8-2 are a lot higher than 9-1. But are these odds greater than 11/6 on, to make the drop a better than evens chance? Not having that in my head I went for the restricted choice rule and successfully finessed the 10.
Question to any poster except Spisu. Does my anaysis make any sense? The result was a MP score of 100% in a field of "experts"
Oct 2006: Mission impossible
Soon: Mission illegal
#18

Posted 2016-July-24, 15:19
 Wackojack, on 2016-July-24, 14:37, said:
Wackojack, on 2016-July-24, 14:37, said:
You don't say how many other pairs were in the same contract, but assuming a 2♣ overcall, I assume the reason you got 100% is that the other declarers played the overcaller to be the one with short hearts and were unable to finesse.
#19

Posted 2016-July-24, 17:17
 Wackojack, on 2016-July-24, 14:37, said:
Wackojack, on 2016-July-24, 14:37, said:
If you happen to cash the ace first, it's still better to finesse than play for QJ tight if the other suit split is 3-6. It's a tossup if it's 2-6. Playing for the drop is better if it's 2-7.
But it's substantially better to play the person with long clubs to be short in hearts and cash the K first which is what the other declarers presumably did.
#20

Posted 2016-July-25, 03:06
 Stephen Tu, on 2016-July-24, 17:17, said:
Stephen Tu, on 2016-July-24, 17:17, said:
But it's substantially better to play the person with long clubs to be short in hearts and cash the K first which is what the other declarers presumably did.
Yes all other declares except one cashed K first. Mea culpa. An undeserved top.
Oct 2006: Mission impossible
Soon: Mission illegal

 Help
Help
